Function for Bilinear Interpolation of a 2D Matrix Using Mathcad
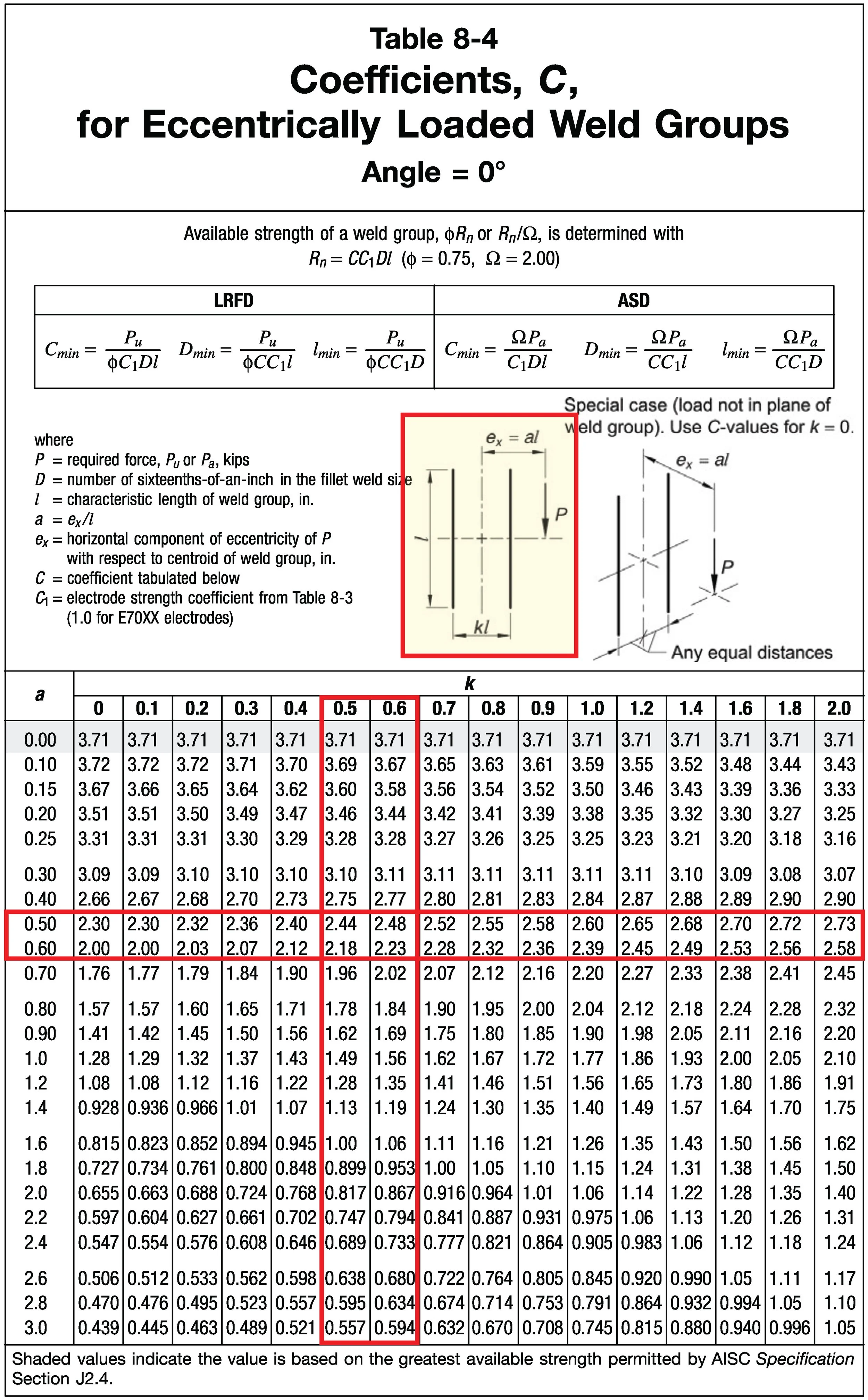
Double, two-way, or bilinear interpolation is commonly encountered in engineering disciplines. Instead of trying to find the value on a line between two points (linear interpolation), bilinear interpolation is used to find intermediate values in a rectilinear grid. A common example is the weld coefficient tables in Chapter 8 of the AISC Manual.
The Function
Mathcad (both v15 and Prime) have a linear interpolation function linterp built in. Bilinear interpolation is a simple extrapolation of linear interpolation, just done in steps. As such, a function that performs bilinear interpolation in Mathcad v15 is
And for Mathcad Prime,
Sample files for these are attached for Mathcad v15 and for Mathcad Prime. If that’s all you need, feel free to click away. Otherwise, next I’ll explain how the function works and go through an example.
How It Works
The first two lines of the function check that the COL and ROW input are vectors (single column, multiple rows) and if not, transposes the values such that they are. Mathcad’s linterp function needs the data to be in vector form.
Consider the following input 2D matrix Mat, with correlating column and row vectors col_vals and row_vals, and values c and r to find the interpolated value for.
The function steps through each column of the input 2D matrix M. For each column, the values are linearly interpolated using the ROW vector as reference, and the interpolated value is stored in new vector N. This continues for each column in M, with subsequent interpolated values being added to vector N.
At the end, vector N is interpolated using the COL vector as reference.
Result = linterp(col_vals , N , c)
Thus,
dlinterp(col_vals , row_vals , Mat , c , r) = 1.49
Design Example
Consider eccentric weld coefficient Table 8-4 of the 15th Ed. AISC Manual, shown below. For this example weld check, the following input values are used:
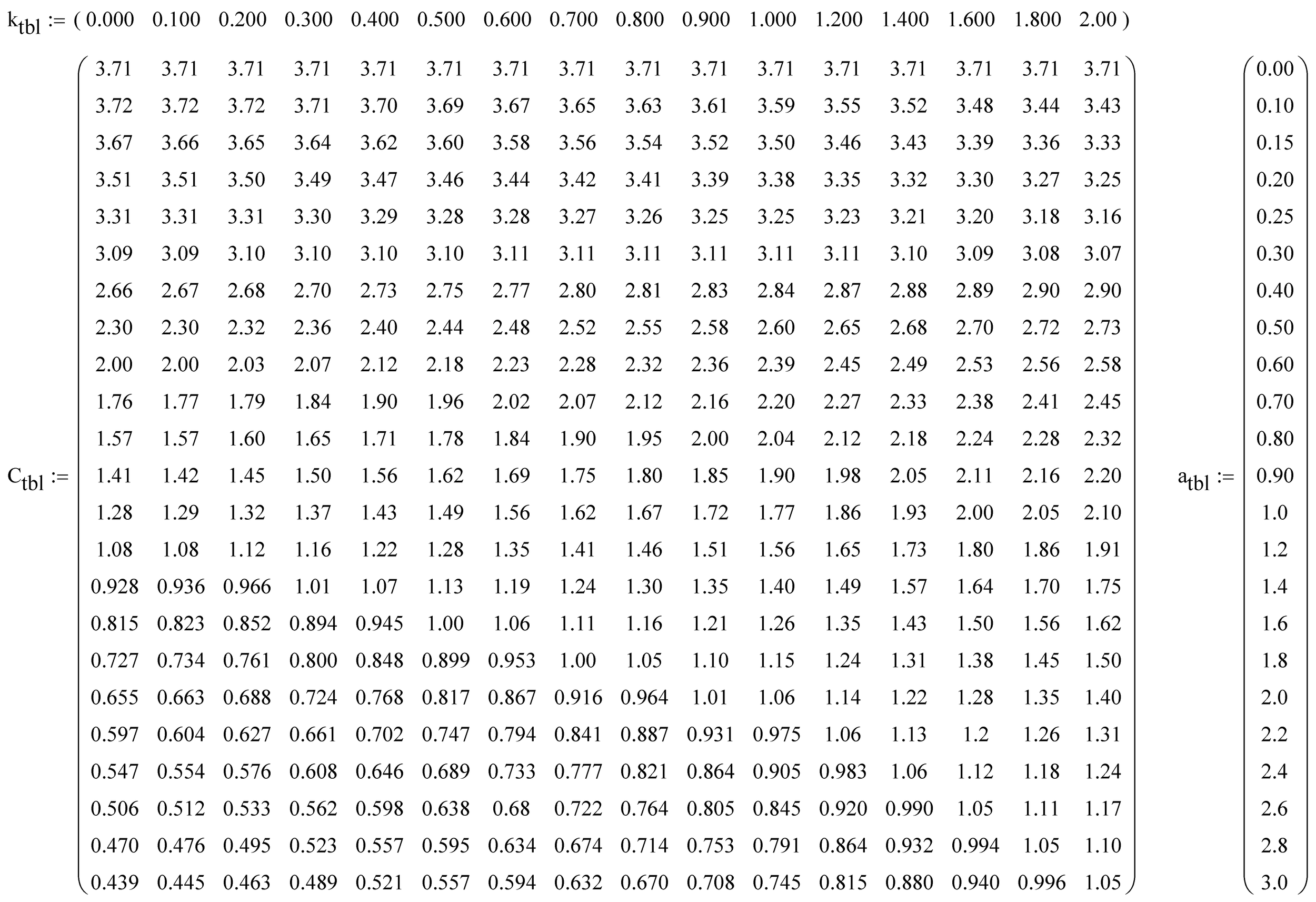
The tabular data from AISC Table 8-4 can be extracted and input to Mathcad as shown below. The row and column vectors are additionally extracted, as these are critical for the interpolation.
The input values are used to determine variables a and k used for interpolation. The resulting interpolated value, and the design of the weld for this example, are as follows.